January Module of the Month: MaZe, Mass-Zero Constrained Dynamics for Orbital Free Density Functional Theory
Description
The program performs Orbital-Free Density Functional Theory Molecular Dynamics (OF-DFT-MD) using the Mass-Zero (MaZe) constrained molecular dynamics approach described in [1].
This method enforces, at each time step, the Born-Oppenheimer condition that the system relaxes instantaneously to the ground state through the formalism of massless constraints. The adiabatic separation between the degrees of freedom is enforced rigorously, and the algorithm is symplectic and time-reversible in both physical and additional set of degrees of freedom.
The computation of the electronic density is carried out in reciprocal space through a plane-waves expansion so that the mass-zero degrees of freedom are associated to the Fourier coefficients of the electronic density field. The evolution of the ions is performed using Velocity-Verlet algorithm, while the SHAKE algorithm is used for computation of the additional degrees of freedom. The code can sample the NVE and the NVT ensemble, the latter through a Langevin thermostat.
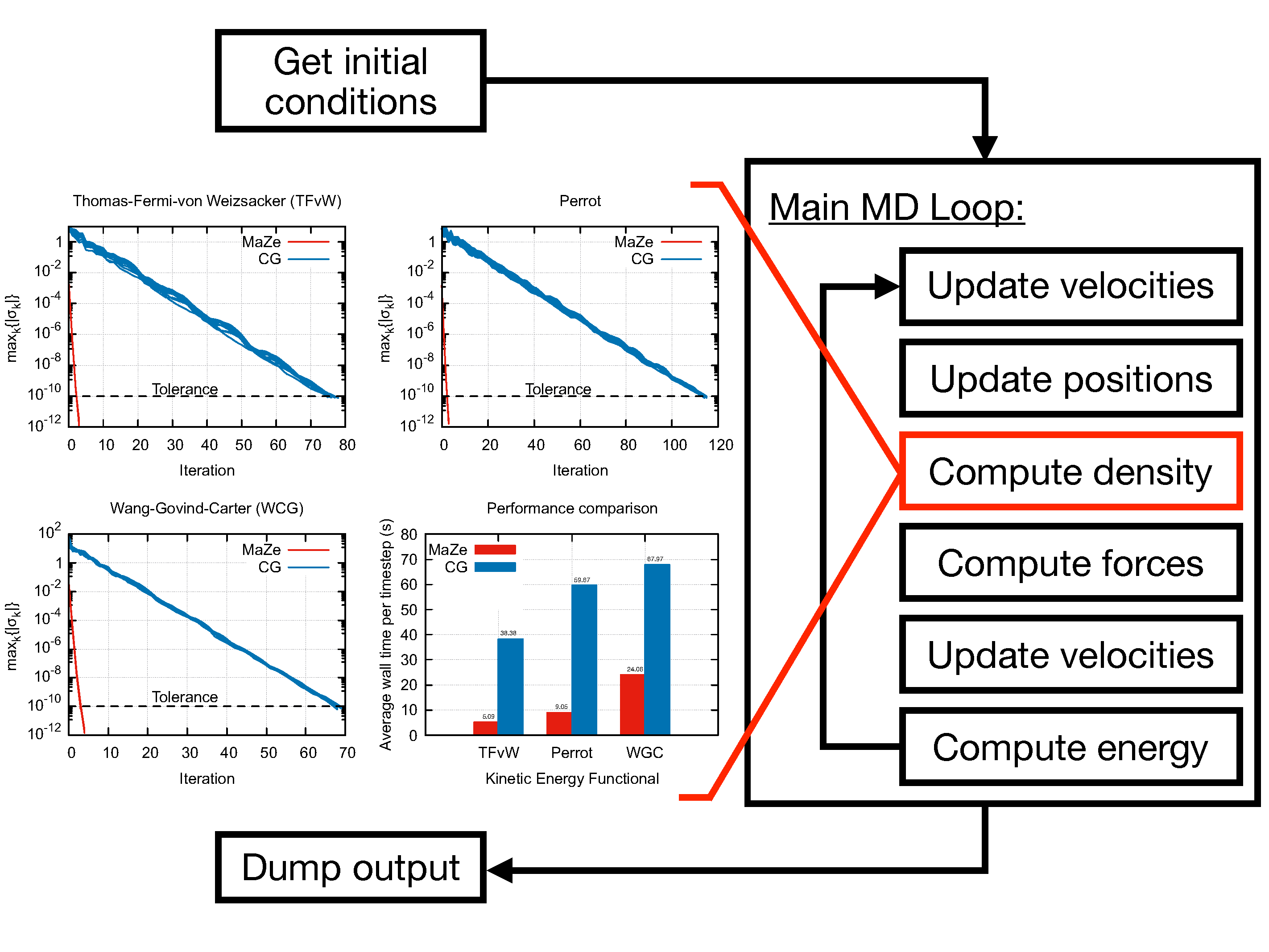
The code was optimised to run on HPC machines, as explained in the software documentation. The proposed optimisations allow a reduction of the execution time by roughly 50% compared to the original version of the code.
Practical application
The code is intended for condensed matter physicists and for material scientists and it can be used for various purposes related to the subject. Even though some analysis tools are included in the package, the main goal of the software is to produce particles trajectories to be analysed in post-production by means of external software.
MaZe implements the orbital-free formulation of density functional theory, in which the optimisation of the energy functional is performed directly in terms of the electronic density without use of Kohn-Sham orbitals. This feature avoids the need for satisfying the orthonormality constraint among orbitals and allows the computational complexity of the code to scale linearly with the dimensionality of the system. The accuracy of the simulation relies on the choice of the kinetic energy functional, which has to be provided in terms of the electronic density alone.
Documentation and source code
The complete documentation is at this location. The source code is available from the E-CAM Gitlab under the MaZe project (software is under embargo until publication leveraging the developments is achieved. Contact code developers or info@e-cam2020.eu for more information.)
References
[1] Sara Bonella, Alessandro Coretti, Rodolphe Vuilleumier, Giovanni Ciccotti, “Adiabatic motion and statistical mechanics via mass-zero constrained dynamics”, Phys. Chem. Chem. Phys. 2020, 22, 10775-10785 DOI: 10.1039/D0CP00163E
Pre-print version (open access): https://arxiv.org/abs/2001.03556