The ALL Load Balancing Library
Abstract
Scalability of parallel applications depends on a number of characteristics, among which is efficient communication, equal distribution of work or efficient data lay-out. Especially for methods based on domain decomposition, as it is standard for, e.g., molecular dynamics, dissipative particle dynamics or particle-in-cell methods, unequal load is to be expected for cases where particles are not distributed homogeneously, different costs of interaction calculations are present or heterogeneous architectures are invoked, to name a few. For these scenarios the code has to decide how to redistribute the work among processes according to a work sharing protocol or to dynamically adjust computational domains, to balance the workload. The A Load Balancing Library (ALL) developed within E-CAM at the Julich Supercomputing Center aims to provide an easy and portable way to include dynamic domain-based load balancing into particle based simulation codes. It provides several schemes to find the ideal split of the workload, from the simplest orthogonal non staggered domain decomposition, to the more fancy Voronoi mesh scheme. Within this text we provide an overview of ALL, its capabilities and current use cases, as well as where to find additional information on the library.
[su_box title=”Library documentation” style=”default” box_color=”#2780BD” radius=”1″]https://gitlab.version.fz-juelich.de/SLMS/loadbalancing
Latest release is 0.9.1 and can be found under: https://gitlab.version.fz-juelich.de/SLMS/loadbalancing/-/releases[/su_box]
[su_box title=”Additional resources ” style=”default” box_color=”#2780BD” radius=”1″]Videos from Webinar on the Load balancing Library, 11th December 2020[/su_box]
Description
Most modern parallelized (classical) particle simulation programs are based on a spatial decomposition method as an underlying parallel algorithm: different processors administrate different spatial regions of the simulation domain and keep track of those particles that are located in their respective region. Processors exchange information
- in order to compute interactions between particles located on different processors
- to exchange particles that have moved to a region administered by a different processor.
This implies that the workload of a given processor is very much determined by its number of particles, or, more precisely, by the number of interactions that are to be evaluated within its spatial region.
Certain systems of high physical and practical interest (e.g. condensing fluids) dynamically develop into a state where the distribution of particles becomes spatially inhomogeneous. Unless special care is being taken, this results in a substantially inhomogeneous distribution of the processors’ workload. Since the work usually has to be synchronized between the processors, the runtime is determined by the slowest processor (i.e. the one with the highest workload). In the extreme case, this means that a large fraction of the processors are idle during these waiting times. This problem becomes particularly severe if one aims at strong scaling, where the number of processors is increased at constant problem size: Every processor administrates smaller and smaller regions and therefore inhomogeneities will become more and more pronounced. This will eventually saturate the scalability of a given problem, already at a processor number that is still so small that communication overhead remains negligible.
The solution to this problem is the inclusion of dynamic load balancing techniques. These methods redistribute the workload among the processors, by lowering the load of the most busy cores and enhancing the load of the most idle ones. Fortunately, several successful techniques are known already to put this strategy into practice. Nevertheless, dynamic load balancing that is both efficient and widely applicable implies highly non-trivial coding work. Therefore it has not yet been implemented in a number of important codes.
The A Load-Balancing Library (ALL) developed within E-CAM at the Simulation Laboratory Molecular Systems of the Juelich Supercomputing Centre, aims to provide an easy and portable way to include dynamic domain-based load balancing into particle based simulation codes. It was created in the context of an Extended Software Development Workshop (ESDW) within E-CAM (see ALL ESDW event details), where code developers of CECAM community codes were invited together with E-CAM postdocs, to work on the implementation of load balancing strategies. The goal of this activity is to increase the scalability of applications to a larger number of cores on HPC systems, for spatially inhomogeneous systems, and thus to reduce the time-to-solution of the applications .

ALL includes several load-balancing schemes, with additional approaches currently being added. The following list gives an overview about the currently included schemes:
- Tensor-Product method: For the Tensor-Product method, the work on all processes (subdomains) is reduced over the cartesian planes in the systems. This work is then equalized by adjusting the borders of the cartesian planes.
- Staggered Grid Method: For the staggered-grid scheme, a 3-step hierarchical approach is applied: work over the Cartesian planes is reduced before the borders of these planes are adjusted; in each of the Cartesian planes the work is reduced for each Cartesian column, these columns are then adjusted to each other to homogenise the work in each column; the work between neighbouring domains in each column is adjusted. Each adjustment is done locally with the neighbouring planes, columns or domains by adjusting the adjacent boundaries.
- Unstructured Mesh Method: In contrast to the Tensor-Product method and the Staggered Grid Method, the unstructured mesh method adjusts domains not by moving boundaries but vertices, i.e. corner points, of domains. For each vertex, a force, based on the differences in work of the neighboring domains, is computed and the vertex is shifted in a way to equalize the work between these neighboring domains.
- Voronoi Mesh Method: Similar to the topological mesh method (Unstructured Mesh Method), the Voronoi mesh method computes a force, based on work differences. In contrast to the topological mesh method, the force acts on a Voronoi point rather than a vertex, i.e. a point defining a Voronoi cell, which describes the domain. Consequently, the number of neighbors is not a conserved quantity, i.e. the topology may change over time.
- Histogram-based Staggered Grid Method: The histogram-based staggered-grid scheme results in the same grid as the staggered-grid scheme (see Staggered Grid Method), this scheme uses the cumulative work function in each of the three cartesian directions in order to generate this grid. Using histograms and the previously defined distribution of process domains in a cartesian grid, this scheme generates in three steps a staggered-grid result, in which the work is distributed as evenly as the resolution of the underlying histogram allows. In contrast to the other schemes this scheme depends on a global exchange of work between processes.
Use cases
ALL is being tested with the HemeLB code[1] from the Centre of Excellence CompBiomed. A recent paper describes how HemeLB’s developments in memory management and load balancing (with ALL) allow near linear scaling performance of the code on hundreds of thousands of computer codes[2].
ALL is implemented in the multi-GPU version of DL_MESO_DPD package (see related news item here). The intention of this integration is to allow for better performance when modelling complex systems with DL_MESO_DPD[3], like large proteins or lipid bilayers, redistributing the work load across the GPUs.
References
[1] D. Groen, J. Hetherington, H.B. Carver, R.W. Nash, M.O. Bernabeu, and P.V. Coveney. Analysing and modelling the performance of the HemeLB lattice-Boltzmann simulation environment. Journal of Computational Science, 4(5):412 – 422, 2013. doi: https://doi.org/10.1016/j.jocs.2013.03.002. // HemeLB URL: www.hemelb.org
[2] McCullough JWS et al. 2021 Towards blood flow in the virtual human: efficient self-coupling of HemeLB. Interface Focus 11: 20190119. doi: http://dx.doi.org/10.1098/rsfs.2019.0119
[3] MA Seaton, RL Anderson, S Metz and W Smith, DL_MESO: highly scalable mesoscale simulations, Mol Simul 39 (10), 796–821 (2013) doi: http://dx.doi.org/10.1080/08927022.2013.772297 // https://www.scd.stfc.ac.uk/Pages/DL_MESO.aspx
December Module of the Month: Load balancing for multi-GPU DL_MESO
Description
This module concerns the implementation of the E-CAM Load Balancing Library (ALL) in the multi-GPU version of DL_MESO_DPD code. The intention is to allow for better performance when modelling complex systems with DL_MESO_DPD, like large proteins or lipid bilayers, redistributing the work load across the GPUs.
ALL provides several schemes to find the ideal split of the work load : Tensor-Product method, Staggered Grid Method, Unstructured Mesh Method, Voronoi Mesh Method and Histogram-based Staggered Grid Method. Due to the orthogonal domain decomposition used in DL_MESO, the Tensor-Product scheme was used, which works well for non-staggered orthogonal meshes.
Practical application
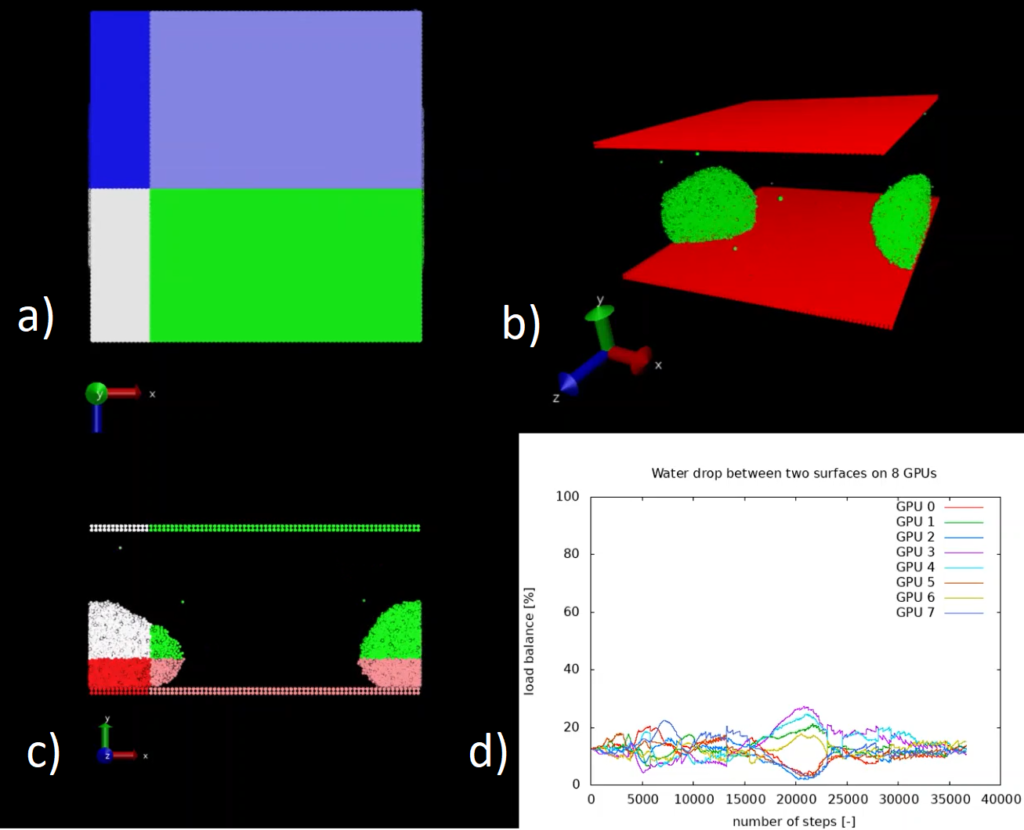
A test case was implemented (see Figure 1 a), b) and c)) that reproduces 32k water beads initially scattered along a regular structure and then slowly agglomerating towards an unique large drop confined between two parallel surfaces. The system is divided across 8 GPUs and, for the purposes of the visualisation, we restrict ourselves to 32k particles. For a larger number of particles it would not be possible to simulate the system without load-balancing, since all the particles agglomerate to a subset of the available GPUs and one or more GPUs would run out of memory having to accommodate a large number of particles. Moreover, such a strong load imbalance drastically reduces the scalability of the application.
In Figure d) we see the time history of the load imbalance for each GPU when using the ALL library. Without load balancing the system would gradually diverge from the ideal value of 12.5%. You can find a video that shows the evolution of the load-balancing for this system in another software module.
Source code
Further details on the implementation of ALL library in DL_MESO and the source code can be found in the E-CAM software repository here.
New article: Quantum Monte Carlo determination of the principal Hugoniot of deuterium
A new article from E-CAM partners at the Maison de la Simulation (CEA, CNRS, Univ. Paris-Sud), have published a new article:
Quantum Monte Carlo determination of the principal Hugoniot of deuterium
Michele Ruggeri, Markus Holzmann, David M. Ceperley, and Carlo Pierleoni
Phys. Rev. B2020, 102, 144108
DOI: https://doi.org/10.1103/PhysRevB.102.144108
Open access version
Abstract: We present coupled electron-ion Monte Carlo results for the principal Hugoniot of deuterium together with an accurate study of the initial reference state of shock-wave experiments. We discuss the influence of nuclear quantum effects, thermal electronic excitations, and the convergence of the potential energy surface by wave-function optimization within variational Monte Carlo and projection quantum Monte Carlo methods. Compared to a previous study, our calculations also include low pressure-temperature (P,T) conditions resulting in close agreement with experimental data, while our revised results at higher (P,T) conditions still predict a more compressible Hugoniot than experimentally observed.
November Module of the Month: PerGauss, Periodic Boundary Conditions for gaussian bases
Description
The module PerGauss (Per iodic Gauss ians) consists on an implementation of periodic boundary conditions for gaussian bases for the Quantics program package.
In quantum dynamics, the choice of coordinates is crucial to obtain meaningful results. While xyz or normal mode coordinates are linear and do not need a periodical treatment, particular angles, such as dihedrals, must be included to describe accurately the (photo-)chemistry of the system under consideration. In these cases, periodicity can be taken into account, since the value of the wave function and hamiltonian repeats itself after certain intervals.
Practical application
The module is expected to provide the quantum dynamics community with a more efficient way of treating large systems whose excited state driving forces involve periodic coordinates. When used on precomputed potentials (in G-MCTDH and vMCG), the model can improve the convergence since smaller grid sizes are needed. Used on-the-fly, it reduces considerably the amount of electronic structure computations needed compared to cartesian coordinates, since conformations that seemed far in the spanned space may be closer after applying a periodic transformation.
Source code
Currently PerGauss resides within the Quantics software package available upon request through gitlab. For more information see the PerGauss documentation here.
Registration open for Extended Software Development Workshop in HPC for Mesoscale Simulation
Few software, like DL_MESO, userMESO and LAMMPS, can currently simulate large Dissipative Particle Dynamics (DPD) simulations. In particular, DL_MESO [1, 2] has recently been ported to multi-GPU architectures and runs efficiently up to 4096 GPUs, an effort supported by E-CAM.
In this E-CAM Extended Software Development Workshop, the developers of the DL_MESO code themselves will provide an introduction to DPD, DL_MESO, its features and functionalities, as well as they will initiate participants to parallel programming of hybrid CPU-GPU systems. Part of the workshop will be dedicated to theory lectures and hands-on sessions on GPU architectures and OpenACC (NVidia DLI course) given by an NVidia DLI Certified Instructor, followed by the practical case of porting DL_MESO to OpenACC.
Interested in participating? Join us on the 18-22 January for this ONLINE course. Express your motivation to attend the workshop directly through the CECAM website at https://www.cecam.org/workshop-details/8
References
[1] DL_MESO is a general purpose mesoscopic simulation package developed at Daresbury Laboratory by Dr. Michael Seaton : http://www.cse.clrc.ac.uk/ccg/software/DL_MESO/
[2] M. A. Seaton, R. L. Anderson, S.Metz, and W. Smith, “DL_MESO: highly scalable mesoscale simulations,”Molecular Simulation, vol. 39, no. 10, pp. 796–821, Sep. 2013
|QBN 〉 Webinar on “Quantum Computing for Material Science and Pharma”
Quantum Business Network |QBN 〉 manages the collaborative processes within the quantum technology ecosystem. The vision of |QBN〉 is to transform the German and the European quantum community to a strong quantum industry.
To support this, |QBN 〉 is organising an interesting webinar and a series of expert meetings on quantum simulations as follows:
- 09.11.2020 QBN Webinar: Quantum Computing for Material Science & Pharma with
- Introduction of the huge potential of quantum computing for material science and pharma
- One hour demo of tools and first steps to simulation real world applications
- 20.01.2021 | 1st QBN Meeting on Quantum Simulation @ HQS Quantum Simulations in Karlsruhe, Germany
- 18.03.2021 | 1st QBN Meeting on Quantum Computing @ Parity Quantum Computing GmbH in Innsbruck, Austria
- 23.03.2021 | 1. QBN Meeting on Quantum Communication @ Tesat-Spacecom GmbH & Co. KG in Backnang, Germany
To learn more about |QBN 〉 and register to their events, visit their website at https://quantumbusinessnetwork.de/en/.