The porting of DL_MESO_DPD [1,2] to graphic cards (GPUs) was reported in deliverable D4.2 of E-CAM[3] (for a single GPU) and deliverable D4.3 [4] (for multiple GPUs) (Figure 1), and has now been extended to include electrostatics, with two alternative schemes as explained below. This work was recently reported on deliverable D4.4[5].
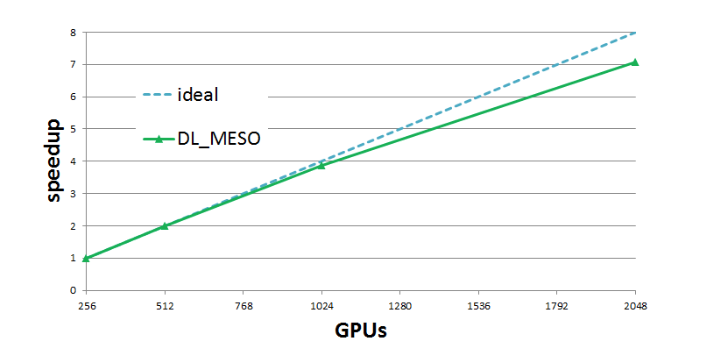
Figure 1: DL_MESO strong scaling results on PizDaint, obtained using 1.8 billion particles for 256 to 2048 GPUs. Results show very good scaling, with efficiency always above 89% for 2048 GPUs.
To allow Dissipative Particle Dynamics (DPD) methods to treat systems with electrically charged particles, several approaches have been proposed in the literature, mostly based on the Ewald summation method [6]. The DL_MESO_DPD code includes Standard Ewald and Smooth Particle Mesh Ewald (SPME) methods (in version 2.7, released in December 2018). Accordingly, here the same methods are implemented for the single-GPU version of the code.
1. Ewald method for the GPU version of DL_MESO_DPD
The Ewald method consists in dividing the long range electrostatic forces in two parts: a short range part, solved in the real space, and a long range one, solved in the reciprocal space. An error weight function combines the two contributions.
Module description
The module consists of several files where the short and long ranges implementations are ported from FORTRAN to CUDA-C language. No changes in the algorithm are required to adapt the code to GPU architectures. However, the memory locality imposed by the Ewald Summation algorithm, proportional to the maximum reciprocal space vector size kmax, could be an issue for performance optimization and it has not been currently investigated. As the short range force subroutines are very similar to the soft potential force, a duplication of the kernel has been avoided allowing to reuse the same one, but with a different cut-off radius.
Motivation and exploitation
The electrostatic force calculation represents usually the main computational costs in systems where even a small amount of charged particles is present (> 1%). Being the main loop and short range force calculation offloaded to the GPU, leaving the Ewald algorithm on CPU would have a double negative impact on the performance: all data should migrate from device to host and vice-versa. Porting to GPU the full short and long range interactions allowed to maintain the speedup factor of 4 when compared to the a traditional Intel 12-core.
A typical industrially relevant example for DPD which includes electrical charges would be a system with water, oil and surfactants. In this line, we considered a simulation of water with SDS (Sodium dodecyl sulfate), a surfactant used in many cleaning products[7] . A system of 192 x 103 particles of which 1152 are charged has been simulated (using a maximum reciprocal space vector size k_max = 20 in each direction) and compared with the parallel MPI master version. The reported speedup factor is 3.5 when using a Tesla P100 card vs Intel Ivy-Bridge 12-core.
Software documentation can be found in our E-CAM software Library here.
2. SPME method for the GPU version of DL_MESO_DPD
Similarly to the above Ewald summation algorithm, the SPME [8] splits the electrostatic forces in short and long range. Again, the long range force is solved in the Fourier space, but this time the electrical charges are spread on a virtual particle mesh using an interpolation function.
Module description
The module consists of several files ported from Fortran to CUDA-C language. While the implementation of the B-spline for the interpolation function requires adapting it to the GPU architecture, the Fast Fourier Transform (FFT) porting is straightforward. In fact, NVidia released the cuFFT library using the same syntax as FFTW, and for its use one merely needs a change in the header file name (from fftw.h to cufft.h). As the previous module, the memory locality of the method, augmented by the order of spline interpolation, has not been optimized yet.
Motivation and exploitation
The Ewald summation method described above scales with N1.5 at best, where N is the number of charged particles. The SPME allows a better scaling, N * log (N), but requires a stencil domain decomposition (i.e. decomposing the domain along one direction only) to allow the FFTW library scaling with more than 1 core. If this is not used, as in the current master version of DL_MESO_DPD, the FFTW becomes rapidly a bottleneck for scaling across several nodes. On the other side, the porting to a single GPU does not need domain decomposition and the same speedup factor (4, compared to 12-core Intel) is maintained.
The SDS-water system (192 x 103 particles) has been simulated and compared with the parallel MPI master version for 3 different maximum reciprocal space vector sizes: 20, 40 and 100 (uniform in each direction). A spline of 8th order has been used. The speedup factor reported is 5 when using a Tesla P100 card vs Intel Ivy-Bridge 12-core. The most important advancement to note is that this speedup would be the same even if more cores were used with the master version. This is due to the missing stencil domain decomposition mentioned above.
Software documentation can be found in our E-CAM software Library here.
Bibliography
[1] http://www.cse.clrc.ac.uk/ccg/software/DL_MESO/
[2] M. A. Seaton, R. L. Anderson, S. Metz, and W. Smith, “DL_MESO: highly scalable mesoscale simulations,” Molecular Simulation, vol. 39, no. 10, pp. 796–821, Sep. 2013
[3] B. Duenweg, J. Castagna, S. Chiacchiera, and H. Kobayashi, “Meso– and multi–scale modelling E-CAM modules I,” Oct. 2017. [Online]. Available: https://doi.org/10.5281/zenodo.1207372
[4] B. Duenweg, J. Castagna, S. Chiacchiera, H. Kobayashi, and C. Krekeler, “Meso– and multi–scale modelling E-CAM modules II,” Mar. 2018. [Online]. Available: https://doi.org/10.5281/zenodo.1210075
[5] B. Duenweg, J. Castagna, S. Chiacchiera, and C. Krekeler, “Meso– and multi–scale modelling E-CAM modules III,” Jan. 2019. [Online]. Available: https://doi.org/10.5281/zenodo.2555012
[6] M. González-Melchor, E. Mayoral, M. E. Velázquez, and J. Alejandre, “Electrostatic interactions in dissipative particle dynamics using the Ewald sums,” The Journal of Chemical Physics, vol. 125, no. 22, p. 224107, 2006.
[7] For a recent study of micelle formation in this mixture within a DPD approach see:
R. L. Anderson, D. J. Bray, A. Del Regno, M. A. Seaton, A. S. Ferrante, and P. B.Warren, “Micelle formation in alkyl sulfate surfactants using dissipative particle dynamics,” J. Chem. Theory Comput., vol. 14, p. 2633, 2018
[8] U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee, and L. G. Pedersen, “A smooth particle mesh Ewald method,” The Journal of Chemical Physics, vol. 103, no. 19, pp. 8577–8593, 1995
