The software
DL_MESO_DPD, is the Dissipative Particle Dynamics (DPD) code from the mesoscopic simulation package DL_MESO[1], developed by Dr. Michael Seaton at Daresbury Laboratory (UK). This open source code is available from Science and Technology Facilities Council (STFC) under both academic (free) and commercial (paid) licenses.
DL_MESO_DPD models particles along with a pairwise thermostat to ensure Galilean invariance and thus correct fluid behaviour. The particles frequently interact with soft pairwise potentials[2], that allow for larger time steps than those available in classical molecular dynamics while still retaining sufficient chemical detail for mesophase-based structures. The code is capable of modelling a wide range of interactions between particles: various pairwise conservative (van der Waals-like) interactions, bonded interactions and electrostatic interactions with smeared charges. For pairwise interactions, it uses the linked-cell list strategy to find relevant particle pairs efficiently with linear scalability.
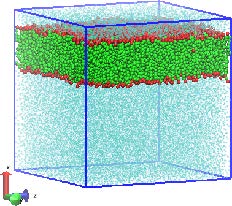
Lipid bilayer formed from self-assembly of amphiphilic molecules in solution, as modelled using DL_MESO_DPD.
The code is modular in structure: similarly functioning subroutines (e.g. pairwise interaction calculations) are grouped together, making it straightforward to find particular functionalities in the code and to add new features. It is well documented: both a user manual and a descriptive article [1] are available.
What can the software do?
DL_MESO_DPD can model a variety of non-bonded interaction potentials between particles. Specifically, it has implemented a Standard DPD model (Groot-Warren) [2] as well as a version of the many-body (density-dependent) DPD [3, 4, 5] , Lennard-Jones[6] and Weeks-Chandler-Andersen [7] potentials, along with the DPD thermostat or alternative pairwise thermostats: Lowe-Andersen [8], Peters [9, 10] or Stoyanov-Groot [11]. A variety of bonded interactions (stretching, angles and dihedrals) are available for representing longer molecules as joined chains of particles. Charges can also be applied to particles and the associated electrostatics calculated using Ewald sums along with either Slater-type (exponential) [12] or Gaussian [13] charge smearing to prevent collapse of soft ions.
Applications within E-CAM
E-CAM’s Work-package 4 (WP4) – Meso- and Multi-scale Modelling, makes use of the DL_MESO_DPD code. Two important applications of this code within E-CAM are :
a) development of algorithms to apply charge dipoles and other multipoles to particles with soft repulsive potentials. This work is in the context of an E-CAM pilot project in collaboration with industry: Polarizable Mesoscale Models ;
b) Improve scalability of the code. In this context, E-CAM has already developed the first GPU version of DL_MESO_DPD code on Nvidia GPUs and this effort will be further developed in the coming months.
New software modules based on DL_MESO_DPD and associated to points a) and b) above were recently reported in deliverable D4.2.: Meso– and multi–scale modelling E-CAM modules I. These codes are also available from WP4 software repository.
Bibliography
[1] Michael A. Seaton, Richard L. Anderson, Sebastian Metz, and William Smith. DL_meso: highly scalable mesoscale simulations. Molecular Simulation, 39(10):796–821, September 2013.
[2] R. Groot and P.B. Warren. Dissipative particle dynamics: bridging the gap between atomistic and mesoscopic simulation. Journal Chemical Physics., 107(3):4423, 1997.
[3] I. Pagonabarraga and D. Frenkel. Dissipative particle dynamics for interacting systems. Journal Chemical Physics., 115:5015, 2001.
[4] S. Y. Trofimov, E. L. F. Nies, and M. A. J. Michels. Thermodynamic consistency in dissipative particle dynamics simulations of strongly nonideal liquids and liquid mixtures. Journal Chemical Physics., 117:9383, 2002.
[5] S. Merabia and I. Pagonabarraga. Density dependent potentials: structure and thermodynamics. Journal Chemical Physics., 127:054903, 2007.
[6] J.E: Jones. On the determination of molecular fields. ii. from the equation of state of a gas. Proceedings Royal Academy London A., 106(738):463, 1924.
[7] J. D. Weeks, D. Chandler, and H. C. Andersen. Role of repulsive forces in determining the equilibrium structure of simple liquids. Journal Chemical Pysics., 54:5237, 1971.
[8] C.P. Lowe. An alternative approach to dissipative particle dynamics. Europhysics Letters., 127:145, 1999.
[9] I. Pagonabarraga, M.H.J. Hagen, and D. Frenkel. Self-consistent dissipative particle dynamics algorithm. Europhysics Letters., 42:377, 1998.
[10] E.A.J.F. Peters. Elimination of time step effects in DPD. Europhysics Letters., 66:311, 2004.
[11] S.D. Stoyanov and R.D. Groot. From molecular dynamics to hydrodynamics: A novel galilean invariant thermostat. Journal Chemical Physics., 122:114112, 2005.
[12] M. González-Melchor, E. Mayoral, M.E. Velázquez, and J. Alejandre. Electrostatic interactions in dissipative particle dynamics using the Ewald sums. Journal Chemical Physics., 125:224107, 2006.
[13] P. B. Warren, A. Vlasov, L. Anton, and A. J. Masters. Screening properties of gaussian electrolyte models, with application to dissipative particle dynamics. Journal Chemical Physics., 138:204907, 2013.
