With Dr. Francesco Fracchia, Scuola Normale Superiore di Pisa
Interviewer: Dr. Donal Mackernan, University College Dublin
Abstract
One quarter to one third of all proteins require metals to function but the description of metal ions in standard force fields is still quite primitive. In this case study and interview an E-CAM project to develop a suitable parameterisation using machine learning is described. The training scheme combines classical simulation with electronic structure calculations to produce a force field comprising standard classical force fields with additional terms for the metal ion-water and metal ion-protein interactions. The approach allows simulations to run as fast as standard molecular dynamics codes, and is suitable for efficient massive parallelism scale-up.
Francesco, could you tell us a bit about yourself, where do you come from originally and what brought you to simulation and to work with E-CAM?
I graduated in Como (University of Insubria), Italy and attended a doctorate in Pisa (University of Pisa) working on the development of the quantum Monte Carlo method, I also worked on the application of the perturbative multireference NEVPT method, at the University of Ferrara. In both cases, these are highly accurate electronic calculation methods, but with limited applicability. I later became interested in optimization algorithms and machine learning methods, and followed some on-line courses from Coursera and Stanford University. E-CAM has given give me the opportunity to apply these techniques to my area of expertise, chemistry, in the pilot project in collaboration with BiKi Technologies [1] on the parameterization of metal ion force fields.
Why is accurate modeling of metal ions interactions with soft matter important in general scientifically and from an industry perspective in particular?
Metal ions play a structural and catalytic role in many enzymes and an accurate description of the interaction with amino acids, nucleic acids, lipids, carbohydrates is essential for the study of biochemical processes. In the industrial field, the accurate description of the behavior of metal ions in soft matter is critical for designing new drugs. A drug in several cases involves the interaction with a catalytic site of an enzyme, binding to it and inhibiting its function. When the catalytic site consists of a metal cofactor, the accurate description of the interaction between the metal ion and the ligand becomes decisive for making predictions about the effectiveness of potential new drugs.
How is E-CAM helping BiKi Technologies [1] to solve this problem?
Since BiKi Technologies provides drug design services to pharmaceutical companies, including parameters and protocols for non molecular dynamics experts, it is in their strategic interest to have tools to generate affordable force fields. Active sites of enzymes include frequently metal ion cofactors. For this reason, an accurate description of these sites is fundamental to perform drug discovery analysis. Unfortunately, available force fields of metal ions proved not to be satisfactory for these applications. We tackled the issue by developing a novel procedure to parameterize metal ion force fields using ab initio data as reference on model systems, and the production of the software tools that exploit this procedure is currently in progress. The outcome of this task should be a novel and general approach to metalloprotein parameterization and a procedure for generating molecular mechanics parameters from quantum chemical potentials. BiKi has collaborated suggesting the protein systems exploited as test cases of the procedure, participating in key discussions and providing computational resources.
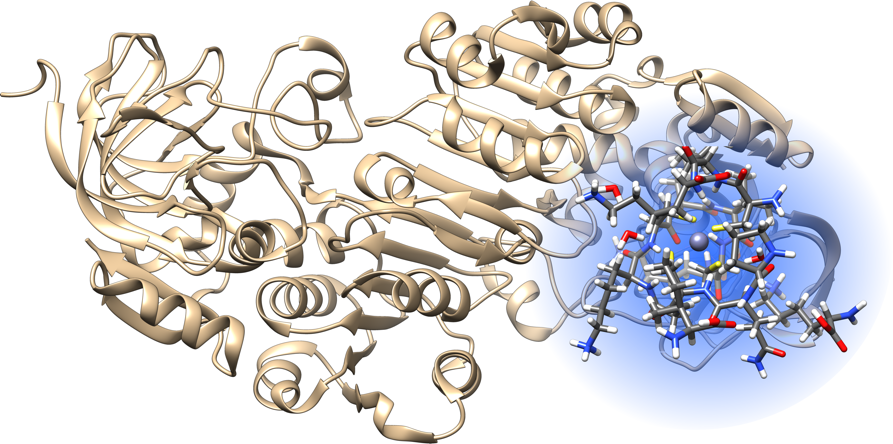
Figure 1: Ab-initio calculations on cluster systems are used as references for the parametrization of the metal ions force fields. The clusters are built cutting protein configurations selected by GRASP sampling.
What are the chief difficulties that accurate simulation has to face? I guess the average molecular force fields may have difficulties treating the metal ion interactions?
The accurate description of the behavior of a metal ion in a biological environment is difficult even using quantum mechanical methods. In fact, in particular for transition metals, only multi-reference methods that include relativistic effects would provide high quality results. However, these methods generally have too high computational cost to be applied to large-sized systems such as a protein. A larger field of applicability can be obtained through QM/MM methods, using DFT for the QM part. Even in these cases, at present the cost of computation is too high to conduct large-scale dynamic simulations in order to obtain structural, thermodynamic and kinetic properties of the systems of interest. Computational costs can be drastically reduced by conducting dynamics with classic models, so it is necessary to develop force fields. For metal ions two alternatives are possible: bonded and non-bonded models. Bonded models can be built to reproduce the desired structural proprieties of the environment of the metal ion but they are not useful to describe the chemistry of the site. In a drug design perspective this is a significant limitation.
Non bonded models can do it, however the parametrization of accurate force fields of this type is more difficult, because the greater structural flexibility of the model can give rise to incorrect coordination of the metal ion. Our work is focused on this particular aspect of the problem: paramaterization of non bonded force fields for metal ions using statistical learning techniques.
Can you can elaborate a little bit more on your approach and explain to what extent it is built on what was there before and to what extent there are new things?
The parametrization of the metal ion force fields is generally conducted trying to reproduce the experimental properties of the ions in water. This is the case, for example, of the force fields produced by Merz and collaborators in numerous works [2], which use the radial distribution functions and the free hydration energies as references. This approach suffers from two difficulties: 1) limited availability of experimental data, often only available for water and other simple polar solvents; 2) little possibility of exploring the space of the parameters of the force-fields. In this case, you can only use a limited functional form for the force-field. If the force fields is not flexible enough, the performance will not be high.
The use of references calculated with ab initio methods to perform the fitting of the force fields allows to:
- explore a much larger parameter space, also using more flexible functional forms than simpler models such as Lennard-Jones
- to exercise greater control over the types of systems to be used as a reference, in particular to generate molecular structures representative of systems similar to those in which force fields will be used.
In our methodology we use ab initio energies and forces of model systems as reference quantities. The model systems are clusters in which the metal ion is coordinated by molecules that are different according to the situations that we want to study (solvents or aminoacides). Clusters are generated by applying a combinatorial algorithm that maximizes the dissimilarity of configurations. The fitting is then performed by introducing in the algorithm: input data (geometries of the cluster), output data (ab initio quantities) and the functional form of the force field model. The functional form can be as simple as a Lennard Jones, but we can use more complex forms too. We tackle the supervised learning problem using linear and non-linear parameters simultaneously by combining linear ridge regression and cross-validation techniques with the differential evolution optimization algorithm.
The clusters that are used to generate different environments can be selected to suit the needs of the user. In the present case, to develop and test the procedure we have used metal ions in water as study cases. We have prepared ion-water clusters and conducted ab initio simulations on these model systems, calculating forces and energies, and we generated the parameters applying the procedure already mentioned above.
How many configurations do you need to use? And if users wanted to do this themselves, how difficult would it be practically?
Generally a training set is composed of at least one hundred clusters. The first step is the generation of a dynamics of the system. This can be conducted for a very large system, a complete protein or a box of proteins and water. Usually we have performed the dynamics with Gromacs [3]. The simulation can be conducted using a standard dynamics, or parallel tempering to sample a larger environment of the metal. We extract the frames of the dynamics, and we generate a descriptor for each configuration. The descriptor is a vector, and the vector is built calculating the distances between the metal ions and the other atoms. Then a Gaussian transformation is performed so as to retain only information about atoms close to the metal ion to generate a matrix which is provided to GRASP sampling [4]. Using the Gaussian transformation is an easy way to select very different conformations. This is necessary because the ab-initio calculation we have to do to compute energies and forces is very expensive, and we want to do that for as few confirmations as is possible. Maximizing the dissimilarity maximizes the gain in information needed to parametrize the force field, that is the over-all efficiency of the algorithm.
This approach then should scale very well on a massively parallel machine, as the ab-initio code can be run on completely independent configurations?
Yes, it is true. Also, the combinatorial algorithm (that is the GRASP sampling code) that choose the training set can be parallelized. The largest cost of the procedure is the calculation of ab-initio quantities.
Can you outline the actual structure of the code?
The structure of the algorithm is organized in nine software modules:
- GROMACS Interface*: this module reads GROMACS trajectories, calculates the distances of all atoms from the metal for each configuration, detects permutatively equivalent atoms, breaks the permutation symmetry by ordering equivalent atoms by distance from the metal, performs a Gaussian transformation of the distances, reduces the dimensionality of the vectorized configurations by ordering them for variance of the transformed distances and selecting the first Natoms, and prepares the input for the GRASP Sampling module as a Natoms × Nconf matrix (G-Matrix).
- GRASP Sampling*: this module reads the G-Matrix and selects N(training) configurations maximizing a fitness function through the GRASP[5] algorithm.
- Gaussian_Interface*: for the N(training) configurations selected by GRASP Sampling, this module operates a spherical cut of size selected by the user, locates the chemical residues included in the sphere, saturates them appropriately, prepares the input for the Gaussian Software Package.
- LRR-DE Interface**: it reads the Gaussian output and prepares the input for the LRR-DE [4] algorithm in the form {x,y} for each of the objective required by the user.
- MOO (Multi-Objective Optimization)**: this module optimizes the weights of each objective function by minimizing the Chebychev distance from the utopia point through the simulated annealing algorithm.
- Differential_Evolution*: metaheuristic global optimization algorithm used to optimize the hyperparameters (regularization parameter and non-linear parameters of the force field) minimizing the leave-one-out cross-validation error.
- WLRR**: it calculates the linear parameters, given a set of hyper-parameters, employing the regularized and weighted normal equation.
- LOOCV Error**: it calculates the leave-one-out cross-validation error for a given set of hyper-parameters and linear parameters.
- Test_Module***: it evaluates the performance of the optimized model on an out-of-sample test.
For the particular application for which the algorithm has been formulated the necessary computational resources are not demanding, however some modules can be used for different purposes which require more resources.
* Software modules that are completed and stored in our GitLab repository at https://gitlab.e-cam2020.eu/e-cam/E-CAM-Library
** Software modules that are in progress and will soon be stored in our GitLab repository
*** Future software development plans
Are your codes being tested for real protein/drug environments? Are there plans for tests by a pharmaceutical company?
Tests on real proteins including zinc ion cofactors are actually in progress. We are focused on the alcohol dehydrogenase system because includes a zinc ion coordinated by four cysteine residues, that is a recurring motif in proteins. The uniform environment of the ion allows to extend gradually the work performed in water to a heterogeneous system. We have also collected data for the carbonic anhydrase II, thermolisin, L-rhamnose isomerase and the zinc finger motif. In this phase we are having difficulty in reproducing the stability of the conformations of the studied metal ions environments. When the generated force fields meet quality requirements in terms of agreement with the experimental data we will pass the complete code to BiKi.
So one could run a simulation and at some reasonable frequency, say every 10 picoseconds, interrupt the simulation and perform the test which make the whole thing tractable and not so expensive?
Yes, that is correct. Such functionality is not yet in the code, but could be easily done.
Could the approach benefit from the use of rare event methods to generate the training set, and for production runs ? That would be a nice example of E-CAM workpackages 1 (basically rare-event methods) and work-package 2 (electronic structure) working together.
Yes, in this direction we currently use parallel tempering to generate the training set but the rare-event methods might produce more relevant dynamics at constant temperature. I agree that this could be an interesting thing to do.
Can people add additional functionality to your codes and what would they need to do?
Additional functionalities can be introduced to interface the algorithm with programs other than Gaussian and GROMACS which at present are used to perform quantum-mechanical and molecular dynamics calculations. Furthermore, other ab initio quantities can be used as references for fitting, in addition to forces and energies, in this case the user should develop a proper interface to prepare the data for the fitting. The preparation of these new features is relatively simple because it only involves the preparation of input and output data for the algorithm.
What do you think are the future prospects and likely impact of this project ?
In the case of metal ion force field parameters, results have so far only been published for the case of ions in water. The application of the procedure to more complex and more interesting contexts (such as proteins) is still in progress.
Further developments from a methodological point of view will be the production of force fields with more flexible functional forms.
Although the method has been developed to perform parametrizations of force fields of metal ions, it is much more general. It can be used to parameterize force fields of anions and solvents (these potential applications are still being tested by the SNS research group) and intramolecular force fields. I should stress that the methodology is a statistical learning process that optimizes the parameters of pre-established functional forms, so that the resulting model is able to reproduce a dataset used for reference. The method can be used to optimize parameters of models of any kind, a problem that is often encountered both in the physical and social sciences. It is necessary to point out that the accuracy of the estimates is strictly dependent on the flexibility of the model and on his suitability to reproduce a given kind of data.
Are there any publications which describe the method in more detail ?
The statistical method is illustrated in the seminal work “Force Field Parametrization of Metal Ions from Statistical Learning Techniques “[4]. Currently, we have introduced two small variations in the application of the method to proteins: (i) the clusters systems used as reference models in this case must be saturated with -H o -OH moieties; (ii) a more efficient metaheuristic algorithm has been introduced to perform the optimization of the hyper-parameters, namely the basic version of differential evolution (rand/1/bin) [6] has been replaced by Success-history based parameter adaptation for differential evolution [7]. These improvements will be described in next publications.
References – Additional Information
[1] BiKi Technologies (http://www.bikitech.com) addresses big challenges in computational drug design including koff prediction and full flexibility in protein-ligand binding. BiKi’s strategic assets are based on molecular dynamics simulations and related approaches, such as enhanced sampling for free energy and kinetics estimations. Further algorithms developed by BiKi Technologies comprise innovative clustering tools based on machine learning. A multidisciplinary team of Software Engineers and Developers, Computational Chemists and Biochemists bring together knowledge and expertise to maintain and support new molecular dynamics based products for drug design and discovery.
[2] Li P., Roberts B. P., Chakravorty D. K., Merz K. M. Jr., Rational design of particle mesh Ewald compatible Lennard-Jones parameters for +2 metal cations in explicit solvent, J. Chem. Theory Comput., 9, 2733-2748 (2013)
[3] Hess B., Kutzner C., Van Der Spoel D., Lindahl E., GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation, J. Chem. Theory Comput., 4, 435-447 (2008)
[4] Fracchia F., Del Frate G., Mancini G., Rocchia W., Barone V., Force Field Parametrization of Metal Ions from Statistical Learning Techniques, J. Chem. Theory Comput., 14, 255-273 (2018)
[5] Feo T. A., Resende M. G., Greedy randomized adaptive search procedures, J. Glob. Optim., 6 (2), 109−133 (1995)
[6] Storn Rainer, Kenneth Price, Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces, J. Glob. Optim., 11 (4), 341-359 (1997)
[7] Tanabe R., Fukunaga, A., Success-history based parameter adaptation for differential evolution. In Evolutionary Computation (CEC), IEEE Congress on pp. 71-78 (2013)
