Abstract
The ability to accurately determine and predict properties of newly developed polymer materials is highly important to researchers and industry, but at the same time represents a significant theoretical and computational challenge. We have developed a novel multiscale simulation method based on the hierarchical equilibration strategy, which significantly decreases the equilibrium properties calculation time while satisfying the thermodynamic consistency. A number of E-CAM modules was developed and implemented in he ESPResSo++ software package.
Hideki, could you tell us a bit about yourself, where do you come from originally and what brought you to simulation and to work with E-CAM?
Originally, I come from Japan. In my PhD period, I developed a general methodology to perform direct numerical simulations of particle dispersions in a shear flow. This program was included in the software package KAPSEL. In the E-CAM project, I have implemented a hierarchical equilibration strategy for polymer melts into ESPResSo++, in the context of a pilot project in collaboration with Michelin aimed at studying the Rheological Properties of New Composite Materials. This was a chance for me to widen my physics background, while my previous experience with soft-matter simulations and software development fitted quite nicely to the project.
What are the goals of your pilot project and your work towards those goals so far?
Our project aims to study the properties of A-B-A block copolymer melts, i.e. mechanical properties, rheological properties etc., by numerical simulations. Thus, equilibrated configurations must be prepared. However, high molecular weight polymer melts require a long relaxation time which increases, according to de Gennes’ reptation theory, with the third power of the molecular weight. In fact, for technically interesting molecular weights, equilibrated configurations cannot be obtained at all with acceptable computational effort if one uses brute-force Molecular Dynamics. For example, the CPU time for 1000 polymer chains consisting of 2000 monomers each is roughly estimated to be about 4.0 × 106 hours on a single processor (2.2 GHz), just in order to get a single relaxed configuration – of which one however needs very many to obtain meaningful values for material properties. Hence, we need an effective method for decreasing the equilibration time. The multiscale simulation method is a suitable way to do this.
Why is this project important in general scientifically, and from an industry perspective in particular?
The development of a multiscale method for polymer blends and block copolymers (in contrast to a homopolymer melt) is fundamentally new and needs to be based on first-principles theory. Let me try to explain what new challenges come with the new systems. The existing approach [1,2,3,4] is extremely successful in reducing the equilibration time, but it can only be applied to homopolymer melts, which do not exhibit a phase transition (i.e. no phase separation, no microstructure formation). For a homopolymer melt, one “only” has to solve the packing problem of putting chains into a box in such a way that they are neither stretched nor squeezed. This problem is essentially always the same, regardless of the level of the hierarchical tree, and regardless of whether the levels are thermodynamically consistent with each other or not. Therefore such consistency was not strictly enforced in Refs. [1,2,3,4], because it was not needed. For blends and block copolymers the situation is quite different: There one additionally needs to worry about the structure of interfaces between species, and of block copolymer microstructures like e.g. lamellae. These additional structures need to be the same on each level of the hierarchical tree, and this is only possible if the interaction parameters of each level are thermodynamically consistent with each other. Otherwise, one will run into a situation where the system is ordered (or phase-separated) on one level of the tree, but disordered (or homogeneous) on the neighbouring level. This would then very severely hamper the efficiency of the approach, and in fact make it unusable. To find such consistent parameters is only possible by applying advanced statistical-mechanical theory. In short, our development is thus an intellectual challenge in its own right. This is intended to then pave the way to analyse the physical properties (in particular, the mechanical and elastic properties) of novel composite materials that attract the attention of industrial companies. Such materials may be promising ingredients of new products like e.g. efficient and environment-friendly car tires.
How is E-CAM helping Michelin to solve this problem?
For simple polymer melts comprising only a single species of monomers, the group in Mainz had already developed the hierarchical equilibration strategy [1,2]. I have implemented this in the publicly available package ESPResSo++ and thus made it available to be used by industrial researchers. Furthermore, we are working on the generalization of the method to make it applicable to systems that are more relevant to industry, i.e. blends and block copolymers.
What are the chief difficulties that accurate simulation has to face?
Phase separation of polymer blends is driven by thermodynamics. Numerical simulations calculating phase behaviour need to satisfy thermodynamic consistency. Unfortunately, the existing hierarchical strategy violates this – for homopolymer melts one “only” has to solve a packing problem, while thermodynamics is much less relevant. Hence, we need to improve the hierarchical strategy to satisfy thermodynamic consistency. In order to facilitate that, we apply the Integral Equation Coarse Graining (IECG) formalism [5] developed by M. Guenza and collaborators at the University of Oregon.
Can you elaborate a little bit more on your approach and explain to what extent it is built on what was there before and to what extent there are new things?
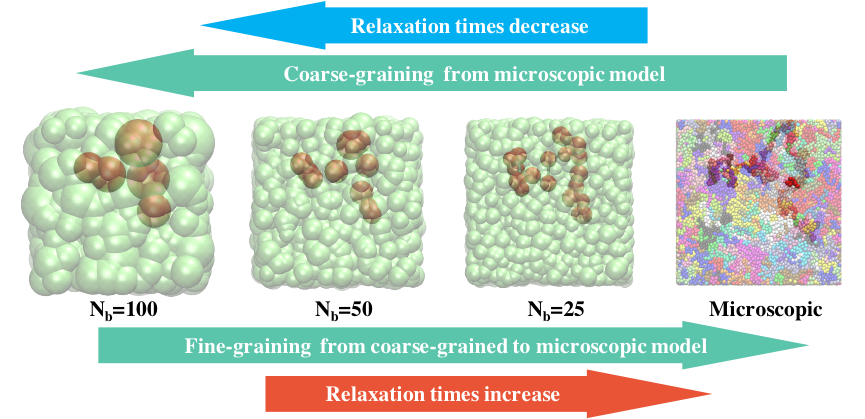
The strategy consists of recursive coarse-graining (CG) combined with sequential back-mapping (or inverse coarse-graining) and can drastically decrease the relaxation time of polymer melts (see Figure 1). The procedure combines a group of several monomers along the chain into one new super-monomer and thus maps a system of high molecular weight onto one with a decreased molecular weight, whose relaxation time is much shorter. For the inverse process, relaxation is only necessary on a local scale and therefore fast as well.
Figure 1: Schematic illustration of the hierarchical equilibration strategy.
The super-monomers or softblobs are represented by the model developed by Vettorel [6]. The softblobs are linked by a harmonic bond potential and an angular bond-bending potential that provides some stiffness. The interactions between non-bonded blobs are taken into account by an IECG potential, i.e. the effective interaction calculated within the framework of the formalism developed by the Oregon group [5]. Therefore, the relaxation time is not only decreased because of the lower molecular weight, but also because of the softened interactions, which allow the chains to easily pass through each other.
After equilibrating a configuration at very coarse resolution, each CG polymer chain is replaced with a more fine-grained (FG) chain. In this back-mapping procedure, a CG blob is divided into several FG blobs. The centre of mass of the FG blobs coincides with the position of the CG blob’s centre and is being kept fixed during the relaxation of the local conformation of the FG monomers within the CG blob. Consequently, a microscopic equilibrated configuration can be reproduced by sequential back-mapping.
A good test that checks if the hierarchical method does indeed provide correctly equilibrated configurations consists of a comparison of results with those obtained from brute-force MD (which is feasible for molecular weights that are not too high). Here in turn one needs to pick a quantity which is very sensitive to distortions of the chain conformations, relative to their ideal structure, and which also relaxes particularly slowly in brute-force MD. In our experience, a useful set of quantities that satisfies these criteria are the mean square internal distances (MSID) of individual polymer chains. For high molecular weights, where such a direct comparison is no longer possible, we have to rely on the fact that polymer physics tells us unambiguously how to scale up from a low to a high molecular weight, both for structure and for dynamics.
I have implemented all the required functions of this strategy into ESPResSo++, with a total of more than 6,000 source code lines.
Can you outline the actual structure of the code?
We already developed and uploaded 9 modules:
- Hierarchical Strategy for Simple One-Component Polymer Melts: minimize energy
- Hierarchical Strategy for Simple One-Component Polymer Melts: fixed-local-tuple
- Hierarchical Strategy for Simple One-Component Polymer Melts: md-softblob
- Hierarchical Strategy for Simple One-Component Polymer Melts: constrain-com
- Hierarchical Strategy for Simple One-Component Polymer Melts: constrain-rg
- Coarse-Graining: A Component of the Hierarchical Equilibration Strategy for Polymer Melts
- Fine-graining: A Component of the Hierarchical Equilibration Strategy for Polymer Melts
- Reinsertion: A Component of the Hierarchical Equilibration Strategy for Polymer Melts
- Feedback control mechanism: A Component of the Hierarchical Equilibration Strategy for Polymer Melts
Additionally, we plan to submit three more modules about the improved hierarchical strategy satisfying thermodynamic consistency.
Since our modules are written in C++, they can in principle be implemented into other simulation engines, such as LAMMPS or GROMACS. This would require additional wrapper functions for interfacing between the modules and the engines. Since we are presently not very familiar with the detailed structure of these other packages, we do not feel in a position to honestly estimate the difficulty of such an endeavor.
Does your approach scale well or has potential to scale well on a massively parallel machine?
In principle, our approach scales well. ESPResSo++ is a fully parallelized Molecular Dynamics package utilising domain decomposition. However, for the coarse-grained systems, we cannot use a lot of cores: due to the long cutoff distance of the interactions, using too many cores would imply too much communication overhead. The interaction range is of order of the polymer size (i.e. the gyration radius) and therefore always significantly smaller than the overall simulation box size. In other words, we do not have a situation of a truly long-ranged interaction like electrostatics, meaning that advanced techniques like Ewald summation or similar need not (and should not) be applied. Typically, a degree of polymerization N (of the soft model) implies O(N^(3/2)) interactions per softblob to be calculated, as the gyration radius scales as N^(1/2). To alleviate the problem, one may think of a hybrid programming paradigm which combines distributed memory (e.g. MPI) with shared memory (e.g. openMP). This would require a major restructuring of the basic MD engine, and we think it is very questionable that this is worth the effort: One should keep in mind that the CG systems take only a small fraction of the overall computational effort anyway. For the microscopic system, our calculations scale well, at least up to 2048 cores (beyond which we did not yet run tests).
Are your codes already being applied to the systems of interest?
No, not yet. According to our roadmap, we first wish to apply the hierarchical strategy to polymer melts with attractive interactions, then to polymer blends and finally to A-B-A block copolymer melts. Polymer melts with attractive interactions are running already. Now, we start to tackle the polymer blend systems.
Can people add additional functionality to your codes and what would they need to do?
According to the ESPResSo++ guidelines, everyone can add a new potential. Other functionalities also can be added in a similar way. This only requires knowledge of C++, Python and MPI computing. However, people who need to modify the core part of the molecular dynamics simulations must read all source code and have strong working knowledge of MPI computing. On the other hand, ESPResSo++ has been written in such a way that this latter situation is avoided as much as possible. In fact, modification of the core “deep down” has proven necessary only very rarely, and we believe that this is a major strength of the package.
What do you think are the future prospects and likely impact of this project?
The original goal of doing computational materials design for non-trivial dense polymer systems was ambitious and is perhaps more ambitious than originally anticipated. Nevertheless, I think that it is achievable, however only with significant additional effort with respect to both fundamental theory (here we are on a good track) and with respect to coding.
Are there any publications which describe the method in more detail?
We have plans to submit two papers: One paper shall describe the implementation of the hierarchical strategy into ESPResSo++, while the other shall focus on the improved hierarchical strategy satisfying thermodynamic consistency.
References
[1] Murat M., Kremer K., From many monomers to many polymers: Soft ellipsoid model for polymer melts and mixtures, J. Chem. Phys., 108, 4340, (1998)
[2] Eurich F., Karatchentsev A., Baschnagel J., Dieterich W., Maass P., Soft particle model for block copolymers, J. Chem. Phys., 127, 134905, (2007)
[3] Zhang G., Moreira L. A., Stuehn T., Daoulas K. C., Kremer K., Equilibration of High Molecular Weight Polymer Melts: A Hierarchical Strategy, ACS Macro Lett., 3, 198, (2014)
[4] Zhang G., Stuehn T., Daoulas K. C., Kremer K., Communication: One size fits all: Equilibrating chemically different polymer liquids through universal long-wavelength description, J. Chem. Phys., 142, 221102, (2015)
[5] Dinpajooh M., Guenza M. G., On the Density Dependence of the Integral Equation Coarse-Graining Effective Potential, J. Phys. Chem. B, 122, 3426, (2018)
[6] Vettorel T., Besold G., Kremer K., Fluctuating soft-sphere approach to coarse-graining of polymer models, Soft Matter, 6, 2282, (2010)