Abstract
A quantum logic gate is one of the key components of the quantum computer, and designing an effective quantum universal gate is one of the major goals in the development of quantum computers. We have developed a software based on local control theory to design efficient state preparation control pulses for universal quantum gates which drive full population transfer between qubit states.
Momir, could you tell us a bit about yourself, where do you come from originally and what brought you to simulation and to work with E-CAM?
I come from Croatia, where I also did my PhD on simulations of nonradiative deactivation processes in photoexcited peptides and other molecular systems using a code for nonadiabatic molecular dynamics which I also developed. E-CAM provided a unique opportunity to learn and further improve my skills in code development and simulations by doing a postdoc on simulating nonadiabatic processes within a real quantum computer in a collaboration with IBM.
What are the goals of your pilot project? Why is this project important in general scientifically, and from an industry perspective in particular, and how is E-CAM helping the industrial partner to solve this problem?
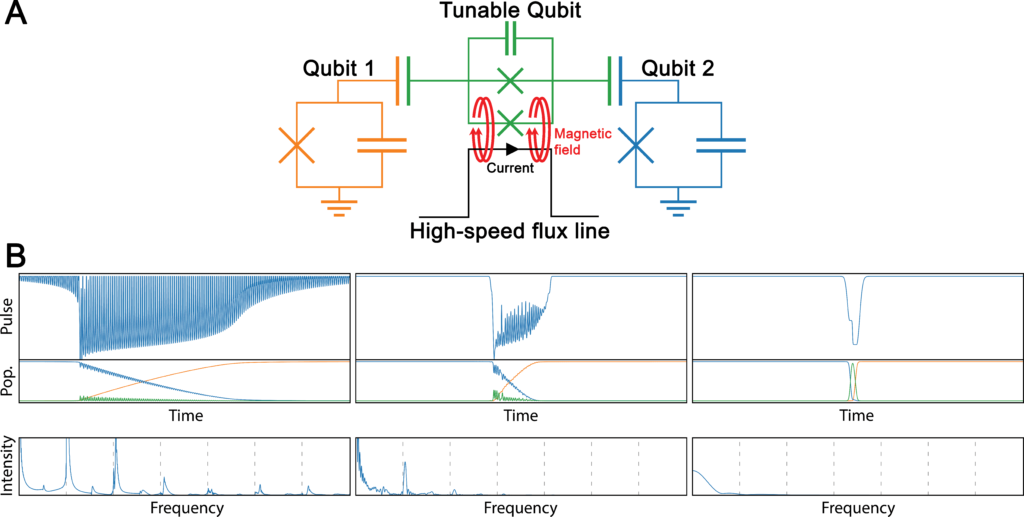
The aim of this pilot project was to develop a new method and dedicated software for designing control pulses to manipulate qubit systems (see Figure 1A) based on the local control theory (LCT),[1] an approach previously used to steer chemical reactions.[2] The system is composed of two (but could be more) fixed frequency superconducting transmon qubits (Q1 and Q2) coupled to a tunable qubit (TQ) whose frequency is controlled by an external magnetic field generated by an electric current through a high-speed flux line. Changing the frequency, the TQ behaves as a targeted quantum logic gate, effectively enabling an operation on the qubit states.[3] The system schematizes an approach to construct real quantum universal gates currently investigated by IBM. In a collaboration with a team at IBM Research Laboratory in Zurich, we have for the first time used LCT to design state preparation pulses which completely transfer population from one qubit to the other. Because real qubit systems are susceptible to decoherence, pulses have to be highly efficient while also very short to compete with decoherence effects. With LCT we have designed extremely short pulses with a duration of just a few tens of nanoseconds or less with an almost full fidelity (see Figure 1B). The method is highly robust and requires only qubit parameters (frequencies, coupling terms) as inputs, and can generate state preparation pulses between any number of qubits in just one evolution of the full system. E-CAM contributed to the theoretical developments in the project, and to the production of software for efficient generation of state preparation pulses.
Can you elaborate a little bit more on your approach and explain to what extent your software is built on, what was there before and to what extent there are new things? What were the chief difficulties you encountered?
The main theoretical tool used, LCT, originates from physical chemistry where it is used to steer chemical reactions towards predetermined products,[2] but it had never been used to design a quantum gate. To create the software, we added entirely new functionalities, geared towards efficiency and reliability, to the open source QuTip program package. As for the difficulties, they were mainly theoretical. LCT generates a required pulse on-the-fly, meaning that at every propagation step of the system evolution it determines the pulse which monotonically transfers population from an initial to a designated target state. Because everything is accomplished in just one system evolution, no approximations of the full system Hamiltonian are required and this is the main advantage of the method. A difficulty that did initially arise, however, was that this procedure produced pulses with a very wide frequency bandwidth, making them impractical for direct implementation in the real systems. We solved this by incorporating a frequency filtering procedure and applying an additional LCT construction step which resulted in shorter pulses of reduced bandwidth, with no extra computational cost. Thus, we further extended this procedure in order to generate reversible state preparation pulses that transfer population from initial to the final state and vice versa. Although this procedure resembles an alternative method known as optimal control theory, it is simpler and less expensive to implement. Furthermore, the LCT algorithm assures pulses always transfer population in one direction, and by optimizing the initial pulse shape the reverse transfer can also be obtained. Using these ideas, we were able to construct SWAP logic gate pulses (pulses which unitarily exchange states between two qubits).
Figure 1: A) Schematic representation of the qubit system; B) Pulses obtained by LCT (left), by a frequency filtering LCT procedure (middle), and by analytic function fitted to LCT pulse parameters (right) with their corresponding population transferring from qubit 2 (blue) to qubit 1 (orange), and frequency spectra.
Can you outline the software that you developed during your pilot project? Does your approach scale well or has potential to scale well on a massively parallel machine? Can people add functionalities to your codes and what would they need to do?
Two main modules were developed during the project. The LocConQubit, which implements the LCT and accompanying procedures, and OpenQubit, a patch to the first module which introduces Lindblad master equation propagation scheme into the LCT which also enables direct construction of pulses under the presence of decoherence effects. There are a few more modules but are currently under consideration for patenting. All modules were written in Python and expand the functionalities of the QuTip program package. The procedure is parallelizable in two ways: 1) by parallelizing the underlying wave function propagation method, which at this stage was not done because the studied systems were not difficult to solve, but will be considered for larger systems; 2) by parallelizing the LCT or system evolution tasks. The latter was particularly used in calculating pulse fidelities by distributing system evolutions on multiple cores of the same node by using QuTip’s shared-memory parallelization, which scales reasonably. This will be further parallelized using modern procedures (such as Dask) to enable usage of more processor cores. Since I wrote the modules following E-CAM’s coding guidelines, they are all well modularized and well documented, so I believe that users won’t have much difficulty in incorporating their new functionalities.
Are your codes already being applied to the systems of interest? Are they being tested by the industrial partner?
The developed software was transferred to IBM and they plan to use it in the medium term to construct pulses for their in-house qubit systems. In fact, the pulses we obtained are of too short duration to be currently implemented with their existing electronics. As soon as they upgrade their instrumentation, LCT state preparation pulses should be applied.
What do you think are the future prospects and likely impact of this project?
This project introduced a new procedure for generating control pulses on-the-fly in qubit systems, which is less computationally demanding and might thus open new approaches to pulse constructions. LCT pulse can also serve as initial guess pulses in optimal control theory, or as we have also used them to generate an ultra-short (only 15 ns long) analytic state preparation pulse (see Figure 1B). Following these ideas, it will be possible to design via a set of preliminary simulations even more versatile quantum gates.
Are there any publications which describe the method in more detail?
One publication was recently submitted to Physical Review Applied.[1] It introduces the concepts of LCT for designing pulses in qubit systems, explains the advantages of such an approach as well as the limitations, and gives an example constructed using real qubit parameters. A second paper will follow with further instructions on how to generate a gate pulse using an LCT approach, as well as study its application on systems with more than two qubits coupled to a single TQ.
References
[1] M. Mališ, P. Kl. Barkoutsos, M. Ganzhorn, S. Filipp, D. J. Egger, S. Bonella, I. Tavernelli, Local control theory for superconducting qubits, submitted
[2] B. F. E. Curchod, T. J. Penfold, U. Rothlisberger, I. Tavernelli, Local control theory in trajectory-based nonadiabatic dynamics, Phys. Rev. A 84 (2011) 042507
[3] D. C. McKay, S. Filipp, A. Mezzacapo, E. Magesan, J. M. Chow, J. M. Gambetta, Universal Gate for Fixed-Frequency Qubits via a Tunable Bus, Phys. Rev. Applied 6 (2016) 064007